Si hacemos una búsqueda en Google con las palabras «abusar» y «omeprazol», nos encontraremos con una catarata de sitios cuyo común denominador es reproducir o comentar un artículo y en cuyos títulos se menciona desde «daño neurológico» hasta «demencia» y «anemia».
El artículo en cuestión se titula El peligro de abusar del omeprazol. Se publicó el 11 de diciembre de 2013 en el diario El Mundo, y en él se da cuenta de la relación entre el consumo de omeprazol y la deficiencia de vitamina B12 (el texto completo puede leerse en: http://www.elmundo.es/salud/2013/12/10/52a73e9761fd3ddb698b4590.html).
Está bien escrito, con una prosa ágil, sencilla y agradable, apto para poder transmitir un conocimiento de salud a un público lego, y seguramente es bien aceptado por la mayoría de los lectores.
Pero es una nota periodística sobre un hallazgo científico, está publicada en un medio de difusión masivo y tiene una carga de subjetividad elevada, derivada de la inadecuada interpretación de las conclusiones a que se llega tras la lectura del trabajo de investigación original. Y a ello se suma la utilización de un lenguaje cargado de cierta cuota de magnificación y espectacularidad, lo que lleva a desvirtuar el mensaje y la relevancia del conocimiento adquirido en el trabajo sobre el que está basada la nota.
Se indica como fuente de origen un documento publicado en la revista JAMA sin especificar de cuál se trata, y que tras una búsqueda simple en PubMed resultó ser el siguiente: Lam JR, Schneider JL, Zhao W, Corley DA. Proton pump inhibitor and histamine 2 receptor antagonist use and vitamin B12 deficiency. JAMA. 2013; 310(22): 2.435-2.442.
Al comparar ambos artículos, surgen algunas cuestiones objetables no menores.
Algunas cuestiones objetables
En el artículo del diario El Mundo, en su tercer párrafo, dice textualmente: «Se estima que entre el 10 y el 15% de los adultos mayores de 60 años tienen deficiencia de vitamina B12».
La prevalencia (entre el 10 y el 15%), que además está resaltada en negrita, no figura en ningún lugar en el trabajo científico. El dato más parecido está en la introducción y dice: «Otros estudios han reportado prevalencias de entre el 5 y el 15%, aunque en éstos puede estar sobreestimada». Cita además que «el estudio NHANES halló que un 3,2% de los adultos mayores de 50 años tendrían bajos valores séricos de vitamina B12». En el capítulo de discusión indica que estos datos son comparables con los hallados por los autores y que fueron de un 2,3%. Es a todas luces evidente que lo expresado en el citado párrafo de El Mundo está magnificado.
Un segundo aspecto que merece la pena destacar y de mucha relevancia se refiere a la interpretación que hace de la odds ratio. El periodista no habla específicamente de este indicador, pero en sus considerandos efectúa una lectura de los resultados aportados por éste de una manera equívoca.
En primer lugar, cabe explicar qué es la odds ratio. Es un término bien conocido en el ambiente de los investigadores y, por supuesto, en el de los estadísticos. Se trata de una medida estadística utilizada en muchos estudios epidemiológicos, particularmente en aquellos denominados «de casos y controles».
La odds expresa el resultado del cociente entre aquellos individuos que han experimentado un determinado suceso y los que no. Es una palabra inglesa que tiene varios significados, y hay controversias sobre cuál de ellos es el más adecuado. Se la equipara con el término «probabilidad», pero esto no sería correcto, ya que probabilidad es el cociente entre aquellos individuos que han experimentado un suceso sobre el total de individuos, por lo cual su valor sólo puede estar comprendido entre 0 y 1. También se traduce como «posibilidad», como «puntos de ventaja», etc. En Argentina, la definición más aceptada para odds es la palabra chance.
Prácticamente el primer paso consiste en calcular la odds correspondiente al grupo de los «casos» y hacer lo propio con el de los «controles».
Ratio significa «razón», «cociente» o «división». Entonces odds ratio se obtendría de la división de la odds de los «casos» sobre el de los «controles», se traduciría como «razón de chances» y la interpretación actual de consenso más aceptada es que estaría indicando cuánta más chance tiene un grupo sobre el otro de que se produzca o esté presente el citado suceso.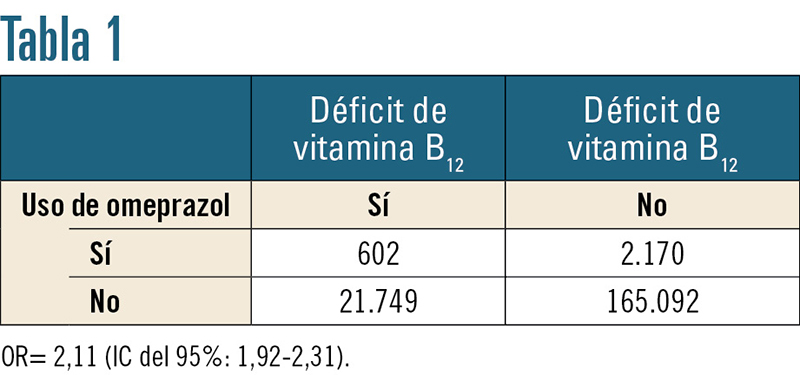 El suceso analizado en el documento científico es el déficit de vitamina B12 y el factor con que se lo relaciona es el uso de inhibidores de la bomba de protones, específicamente el omeprazol, consumido durante 2 o más años y en dosis de más de 1,5 píldoras diarias. Los datos que de allí se obtienen se muestran en la tabla 1.
El suceso analizado en el documento científico es el déficit de vitamina B12 y el factor con que se lo relaciona es el uso de inhibidores de la bomba de protones, específicamente el omeprazol, consumido durante 2 o más años y en dosis de más de 1,5 píldoras diarias. Los datos que de allí se obtienen se muestran en la tabla 1.
Se puede apreciar que el estudio es muy grande, dado el número de individuos comprendidos en él (n= 189.613).
Se trata de un estudio de casos/controles. El grupo de los casos corresponde a aquellos que presentan déficit de vitamina B12. Allí vemos que 602 individuos consumen la cantidad elevada de omeprazol expresada, mientras que 21.749 no tienen ese nivel de consumo, por lo que:
Odds déficit vitamina B12= 602/21.749= 0,028
En tanto que, en el grupo de controles, los que no presentan déficit de vitamina B12, 2.170 individuos, usan la mencionada dosis de omeprazol, y 165.092 no presentan esa condición. Entonces la odds de los no deficitarios sería:
Odds no déficit vitamina B12= 2.170/165.092= 0,013
Por lo tanto, la
Odds ratio= odds déficit/odds no déficit= 0,028/0,013= 2,15
En el artículo científico la odds ratio calculada es de 1,95, ligeramente inferior por los motivos de cálculo estadístico especial que están explicados en él.
De ahí que el artículo periodístico exprese textualmente: «En cuanto a las dosis más peligrosas, se comprobó que tomar diariamente 1,5 comprimidos se asoció a un riesgo un 95% superior a esta deficiencia, comparado con una ingesta diaria inferior a 0,7 píldoras».
El periodista infiere entonces «un riesgo un 95% superior», debido precisamente al valor obtenido de 1,95, que tendría cierta lógica, aunque ésta no es una interpretación correcta, ya que la odds ratio no mide directamente el riesgo.
No es la primera vez que un medio periodístico incurre en errores de esta naturaleza, y todo ello porque suena espectacular referirse a un ¡95%!
Aun considerando el caso de que fuera correcto o discutible que midiera el riesgo, sería necesario hacer otra evaluación dentro del contexto.
¿Es mucho ese porcentaje expresado? ¿Tiene mayor sentido esa expresión? Haciendo otro cálculo, quizá los números adquieran mayor sentido de la realidad, o del impacto.
El porcentaje de individuos con déficit de vitamina B12 y consumo de omeprazol, con respecto al total de los individuos deficitarios, es del 2,8%, y el de los que no presentan déficit representa el 1,3% del total. Dicho en otros términos, según los datos del informe, de cada 1.000 personas con deficiencia de vitamina B12, 28 tenían una alta ingesta de omeprazol, mientras que en el grupo de control habría 13 individuos. Entonces vemos que en este trabajo el grupo «casos» presenta sólo 15 individuos más sobre 1.000 con deficiencia de vitamina B12 con respecto al grupo de «control».
El valor obtenido de la odds ratio nos indica que el resultado del estudio es «estadísticamente significativo», pero evaluando la diferencia de los porcentajes de individuos afectados en los casos y los controles podríamos decir que «epidemiológicamente tiene poca importancia», y finalmente podríamos indicar que este hallazgo es «clínicamente atendible», o sea que debe ser valorado por el médico clínico –y por qué no por el farmacéutico–, pues podría resultar de interés indicar la determinación periódica de vitamina B12 en aquellos pacientes que vienen consumiendo omeprazol desde hace mucho tiempo.
Es indudable que, con esta presentación de los datos, se gana en objetividad y se pierde en espectacularidad. Esta nueva visión de los resultados, en la cual estamos hablando de porcentajes y de números absolutos pequeños, cambia sustancialmente el impacto de los resultados.
Todo ello pone de manifiesto que analizar la odds ratio como número crudo en ocasiones no resulta muy útil, ya que si no se analizan los porcentuales de pacientes afectados esa «razón de chances», incluso en los casos en que sea muy alta, a efectos prácticos puede no estar significando nada importante.
El título del artículo es, como se indicó al comienzo, El peligro de abusar del omeprazol. Está dando a entender desde el comienzo que existe una relación causa-efecto. La odds ratio nunca proporciona esta información, sino que tan sólo sugiere que «hay asociación». Es interesante observar que lo más apropiado del artículo del periódico es que usa el término «abusar» en el título y en su interior, lo que puede generar en el lector una idea educativa tendente al uso racional del medicamento.
Una noticia como ésta, llevada a la masa popular, probablemente genere angustia, preocupación, pérdidas de adherencia al tratamiento y el consecuente riesgo de incremento de las patologías gástricas, lo que podría contrarrestar los excelentes logros obtenidos en las últimas décadas por los inhibidores de la bomba de protones.
Hay otro trabajo muy bueno realizado en Canadá (Targownik, CMAJ, 2008) que estudia la relación entre el consumo persistente de inhibidores de la bomba de protones y el riesgo de fracturas relacionadas con la osteoporosis, y en el que se observa una relación positiva con resultados estadísticos similares. En su conclusión, sus autores, muy cautamente, indican la asociación encontrada y sugieren que hay que continuar los estudios para determinar la importancia clínica del hallazgo.
Es muy «saludable» que los profesionales de la salud, al menos, tengan acceso al conocimiento genuino y expresado con la objetividad y la mesura adecuada, de ahí que debamos tener especial precaución cuando temas referidos a la salud no son abordados por especialistas en el área.
No es mi intención en este texto denostar la actividad periodística. Por el contrario, creo que, cuando fuera posible, sería interesante y de lo más fecundo realizar un trabajo mancomunado, asesorando a periodistas de cualquier nivel, pues estos profesionales constituyen unos aliados fundamentales para el proceso de educación en salud para la población.
Nota del autor
Agradezco la colaboración de Laura Zingaretti, profesora en Matemáticas (Docente Univ. Nac. Villa María) y maestranda en Estadística, por la lectura analítica de los considerandos estadísticos.