Piense en un caso posiblemente real. Después de haber leído algún estudio sobre la importancia de la revisión de los tratamientos en pacientes mayores polimedicados, hemos querido iniciar un estudio similar en nuestra farmacia.
Dado que hay dos farmacéuticos en ella, no es posible plantear la creación de un grupo control en donde no se implemente ninguna intervención. Para evitar incrementar el trabajo del farmacéutico adjunto, él se encargará del grupo control manteniendo la metódica habitual en la farmacia, mientras que el titular realizará la intervención.
El estudio se inicia recibiendo el titular a los pacientes y asignándolos a uno u otro grupo. Cuando se alcanza el número de pacientes que se había estimado como tamaño mínimo de muestra, el adjunto analiza algunas variables de cada grupo, entre ellas la edad y el número de fármacos, observando que su grupo, el de control, tiene una menor edad media, así como un número menor de fármacos por paciente que el del grupo de intervención, conducido por el farmacéutico titular. Comentando entre ellos si esa diferencia tiene importancia o no, el titular indica que, por motivos éticos, había asignado a los pacientes más polimedicados al grupo de intervención, tras considerar que sería más conveniente que ellos se beneficiaran de la intervención pues, en principio, presentarían un mayor riesgo de problemas relacionados con los medicamentos. Sin embargo, pronto descubrirán que han cometido un importante sesgo de inclusión selectiva al asignar de forma no aleatoria a los pacientes, de modo que los dos grupos no son homogéneos. En dicho caso, la validez interna del estudio (grado en que los resultados observados pueden atribuirse a la intervención) se habrá visto reducida.
¿Cómo obtener grupos homogéneos?
Dado que siempre pueden existir variables que no podemos controlar, pero que pueden afectar al resultado final, se precisará que dichas características estén presentes de una forma similar en ambos grupos. Es decir, que el grupo de control tenga una media de edad similar a la del grupo de intervención; que éste integre una proporción similar de pacientes con cardiopatías que el grupo control; que el grupo control, a su vez, tenga un porcentaje similar de mujeres, etc. Es decir, que ambos sean equivalentes en cuanto a todas las variables relevantes.
Para lograr esta homogeneidad, se precisa que dichas variables sean distribuidas mediante el azar. Sólo así (y partiendo de un tamaño de muestra adecuado) el resultado final podrá atribuirse a la intervención. En caso contrario, no habrá garantías de asociar dicho resultado a la intervención. Esta asignación, aleatoria o no, es la que determina si el estudio es experimental (de gran validez interna) o no experimental, respectivamente.
La asignación aleatoria de los pacientes
Antes de asignar al paciente a un grupo u otro, éste deberá haber cumplido con los criterios de inclusión, no haber sido motivo de exclusión por algún otro criterio y haber dado su consentimiento informado a participar en el estudio. Es después de todo ello cuando se asigna al paciente a un grupo, y no antes.
Se describen los tipos de asignación aleatoria más importantes para que el lector pueda llevarlos a cabo de forma sencilla. Es importante indicar que existen métodos que, aunque parecieran válidos, no lo son porque no responden a la definición de «distribución por azar». Así, no puede incluirse al paciente en un grupo u otro en función del día u hora de su incorporación. Los lunes o las primeras horas de la mañana, por ejemplo, podrían estar asociados a una mayor o menor proporción de cierto tipo de pacientes.
Aleatorización simple
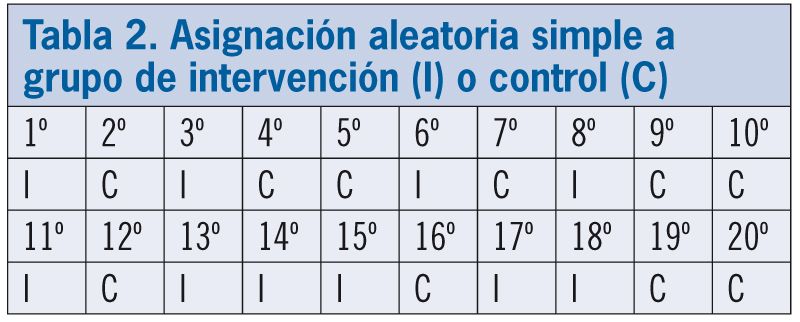
La aleatorización simple es el método más sencillo y útil. Aunque el tamaño de muestra debe ser calculado (y debería ser mayor que el del ejemplo), imaginemos para simplificar la cuestión que se precisan 10 pacientes en cada grupo, 20 en total. Se inicia el proceso generando una tabla de números aleatorios sin repetición, del 1 al 20, y decidiendo a priori que la misma será leída, por ejemplo, de izquierda a derecha. Se decide también a priori que, por ejemplo, los números pares se asignan al grupo de intervención y los impares al de control. Una vez concluido el proceso, en este ejemplo (tabla 1) la asignación aleatoria simple de pacientes quedaría como se indica en la tabla 2. Es decir, el primer paciente se asignará al grupo de intervención, el segundo al de control, el tercero al de intervención, el cuarto y quinto al de control, etc.

Aleatorización por bloques
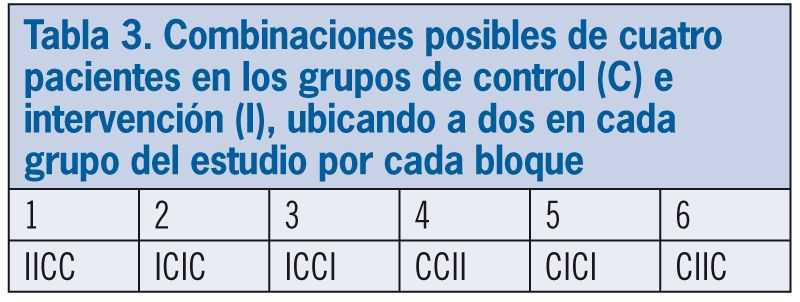
Si se precisa que el número de pacientes asignados a cada grupo sea similar a lo largo del estudio, éste es el método que debe plantearse. Para efectuarlo, y siguiendo con la muestra anterior, ésta se dividirá entre el número de pacientes que se desee que haya en cada bloque, por ejemplo 4 por bloque. Ello implica que la muestra se dividirá en cinco bloques de 4 pacientes cada uno. Asimismo, se decide cuántos pacientes de cada bloque se asignarán al grupo de intervención y al de control, por ejemplo, 2 pacientes en cada bloque. A continuación, se representan y enumeran las posibles combinaciones existentes en cada bloque, teniendo en cuenta que se ha decidido que los bloques sean de 4 pacientes, 2 de ellos en el grupo control y los otros 2 en el de intervención (tabla 3). Finalmente se genera una tabla de cinco números aleatorios con repetición, uno por bloque (tabla 4), a partir de los seis bloques numerados, obteniendo así una secuencia determinada que marcará la asignación de los pacientes en cada uno de los cinco bloques en que se dividió la muestra (tabla 5).


Aleatorización estratificada
A veces se requiere que alguna variable (que pueda ser notablemente responsable del resultado final) esté distribuida homogéneamente con certeza. Por ejemplo, sospechamos que el sexo puede tener influencia sobre el resultado de la intervención en función de si el grado de polimedicación es elevado o no. Para asegurar esto, la muestra se dividiría en dos estratos, hombre y mujer, y a cada uno de ellos en dos subsustratos, de 0 a 4 fármacos y de 5 en adelante. Finalmente, se procede a una asignación aleatoria simple, como se indicó previamente, a los grupos de intervención y control en cada uno de los cuatro subestratos (hombre poco polimedicado, hombre gran polimedicado, mujer poco polimedicada y mujer gran polimedicada).
Aleatorización por conglomerados o «clústers»
En muchas ocasiones, se precisa que el grupo de intervención se ubique en un lugar diferente que el control, para evitar la contaminación del profesional que, al conocer el potencial beneficio de la intervención, no efectuará un cuidado usual exacto en el grupo control. Con este fin se separan físicamente las unidades de estudio, por ejemplo en farmacias diferentes. De esta manera, la unidad de asignación la forman los grupos, y no los individuos. Así, la asignación aleatoria, simple o por bloques, decidirá qué farmacias efectúan la intervención y cuáles no.
Conclusión
Si las variables o características de los integrantes de cada grupo de estudio no son similares, el resultado final puede ser debido a la intervención o a cualquiera de las variables que predominan en un grupo u otro. En ese caso, la validez interna del estudio se habrá visto reducida notablemente, y los resultados obtenidos no serán concluyentes. Es imprescindible distribuir de forma aleatoria a los pacientes con el fin de que cada grupo posea unas características homogéneas. Así, y sólo así, podría concluirse que el resultado obtenido es fruto de nuestra intervención.
El estudio CPATCH1
El estudio CPATCH analiza una intervención realizada en farmacias comunitarias en Canadá con el objetivo de mejorar la adherencia al tratamiento con estatinas. Las 357 de la provincia de Saskatchewan fueron invitadas a participar, procediéndose a una aleatorización por conglomerados, de forma que las farmacias fueron las asignadas a implementar la intervención o el cuidado usual a todos los pacientes que acudieran a cada una de ellas.
Para ello, se generó una lista de 60 números aleatorios con repetición. Asimismo, se describieron y numeraron todas las posibles combinaciones con seis componentes (farmacias), de modo que hubiera igual número de grupos de intervención como de control (tres de cada), por ejemplo: 1, CCCIII; 2, ICCIIC; 3, IICICC, etc. Finalmente, se describió una secuencia de números (los generados aleatoriamente) y su correspondencia con los grupos que designar. Por ejemplo, si la secuencia de números hubiera sido: 3, 1, etc., las farmacias hubieran sido asignadas a los grupos de intervención (I) o control (C) de la siguiente forma: 1.ª (I), 2.ª (I), 3.ª (C), 4,ª (I), 5.ª (C), 6.ª (C), 7.ª (C), 8.ª (C), 9.ª (C), 10.ª (I), 11.ª (I), 12.ª (I), etc.
1Evans C, Eurich D, Taylor J, Remillard A, Shevchuk, Blackburn D. A pragmatic cluster randomized evaluating the impact of a community pharmacy intervention on stating adherence: rational and design of the Community Pharmacy Assisting in Total Cardiovascular Health (CPATCH) study. Trials. 2010; 11: 76
