El problema que habíamos detectado, junto con los médicos del centro de salud correspondiente, fue que una significativa proporción de pacientes hipertensos no seguía adecuadamente su tratamiento. El incumplimiento del tratamiento farmacológico antihipertensivo, la ausencia de actividad física, el exceso de peso y algunos otros aspectos fueron las causas principales observadas que provocaban la falta de control en los pacientes, a pesar de disponer de unas prescripciones correctas. Por ello, el objetivo principal con estos pacientes (la reducción de sus cifras de PAS y PAD, así como el adecuado control de los demás factores de riesgo cardiovascular) no se conseguía en muchos casos. Obviamente, tampoco se podía reducir dicho riesgo y prevenir episodios mortales y no mortales futuros (como infarto agudo de miocardio [IAM] o accidente cerebrovascular agudo [ACVA], principalmente).
Así, una vez desarrollada la intervención a lo largo de un año y tras haber obtenido algunos datos acerca de las variables evaluadas, solo restaba analizarlos y proceder a extraer las conclusiones de nuestro estudio. Sin embargo, surgió un nuevo problema cuando discutíamos la forma en que los datos sobre las variables debían ser manejados. Para concluir que nuestro programa era efectivo, ¿sería suficiente con cualquier reducción de la PAS o la PAD del grupo de intervención con respecto al de control?; si conseguíamos aumentar algo la proporción de pacientes controlados, ¿ello significaba que la efectividad fue positiva? Nuestro último problema, por tanto, era cómo debíamos analizar dichos resultados.
Manejo sencillo de la estadística
En un tema anterior se clasificaron las variables en cuantitativas y cualitativas. Las primeras se expresan mediante números o cantidades. En nuestro caso, la PAS o la PAD, por ejemplo 135/85 mmHg, son variables cuantitativas continuas que pueden tomar cualquier valor. Por su parte, el paciente puede estar o no controlado con respecto a su presión arterial (PA), por lo que el control de la PA será otra variable, esta vez cualitativa o categórica, ya que solo puede pertenecer a dos categorías diferentes y mutuamente excluyentes: controlado o no controlado; así, consideramos como controlados los valores menores de 140/90 mmHg, y como no controlados los que superan dicha cifra.
En el más sencillo de los casos (pero habitual en la investigación en atención farmacéutica), la variable de exposición es cualitativa categórica (intervención o no intervención), y las variables de resultado son cuantitativas o cualitativas. De esta forma, y mediante un software asequible a cualquier persona (Microsoft Excel), pueden analizarse las variables en los casos más frecuentes. Si la variable «resultado» es cuantitativa continua, el análisis estadístico requerido es la prueba de la t de Student, y si es cualitativa, la prueba de la chi al cuadrado.
Diferencia de medias
Si las variables resultado son cuantitativas continuas, como las diferencias entre las reducciones de PAS del grupo de intervención y control, el valor de la disminución debida a la intervención (y su intervalo de confianza [IC] del 95%) se estimará mediante la t de Student.
 Imaginemos que se han obtenido los resultados de PAS de la tabla 1. Primero se calcula la media aritmética mI y mC de los valores de PAS inicial y final de cada grupo, la cual es respectivamente de 152,4 y 142,3 mmHg en el grupo de intervención (I) y 151,1 y 146,6 mmHg en el control (C) (con la función «promedio» de Excel). Seguidamente, se estiman sus desviaciones estándar (DE): 4,1 y 4,1 en el grupo I, y de 4,0 y 4,4 en el C (con la función «desvestp») y sus errores estándar (EE): 0,917; 0,979; 0,898 y 0,983, respectivamente, (siendo EE = DE /√n). Acto seguido, la reducción asociada a la intervención se calcula mediante la diferencia de diferencias (Diferencia = dif.mI _ dif.mc), siendo dif.mI: 9,2, y dif.mC: 4,6 mmHg (dif.m= mini – mfin), por lo que la diferencia global es 4,60 mmHg (Diferencia: 9,2 – 4,6). Finalmente, el IC del 95% de dicha diferencia se estima en el rango: 1,69 – 7,51 (IC del 95%= Diferencia ± 1,96*EEdiferencia), siendo el error estándar de dicha diferencia (EEdiferencia) de 1,485 (EEdiferencia= √ [DEI/nI + DEC/nC]).
Imaginemos que se han obtenido los resultados de PAS de la tabla 1. Primero se calcula la media aritmética mI y mC de los valores de PAS inicial y final de cada grupo, la cual es respectivamente de 152,4 y 142,3 mmHg en el grupo de intervención (I) y 151,1 y 146,6 mmHg en el control (C) (con la función «promedio» de Excel). Seguidamente, se estiman sus desviaciones estándar (DE): 4,1 y 4,1 en el grupo I, y de 4,0 y 4,4 en el C (con la función «desvestp») y sus errores estándar (EE): 0,917; 0,979; 0,898 y 0,983, respectivamente, (siendo EE = DE /√n). Acto seguido, la reducción asociada a la intervención se calcula mediante la diferencia de diferencias (Diferencia = dif.mI _ dif.mc), siendo dif.mI: 9,2, y dif.mC: 4,6 mmHg (dif.m= mini – mfin), por lo que la diferencia global es 4,60 mmHg (Diferencia: 9,2 – 4,6). Finalmente, el IC del 95% de dicha diferencia se estima en el rango: 1,69 – 7,51 (IC del 95%= Diferencia ± 1,96*EEdiferencia), siendo el error estándar de dicha diferencia (EEdiferencia) de 1,485 (EEdiferencia= √ [DEI/nI + DEC/nC]).
Para concluir, es preciso estimar si dicha reducción es estadísticamente significativa. Para ello, en Excel iremos a «Datos – Análisis de datos – Prueba t para dos muestras suponiendo varianzas desiguales», en donde se indicarán los valores de los dos grupos y un nivel de significancia alfa de 0,05. La aplicación muestra que el valor «P, dos colas» es de 0,0036, indicando que no se puede considerar la reducción por el azar, y admitiendo que presenta relevancia estadística. Ello se complementa con la relevancia clínica que posee una reducción de la PAS próxima a 5 mmHg.
Diferencia de proporciones
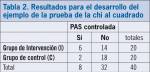 En el caso de variables categóricas (como PA controlada o no), primero estimaremos la frecuencia de resultados obtenidos en cada caso, mediante una tabla de contingencia de valores hallados. Para el ejemplo anterior, los resultados de dicha tabla de contingencia se indican en la tabla 2 que, para simplificar, se han considerado como controlados a los que presentan una PAS >140 mmHg.
En el caso de variables categóricas (como PA controlada o no), primero estimaremos la frecuencia de resultados obtenidos en cada caso, mediante una tabla de contingencia de valores hallados. Para el ejemplo anterior, los resultados de dicha tabla de contingencia se indican en la tabla 2 que, para simplificar, se han considerado como controlados a los que presentan una PAS >140 mmHg.
Si los resultados de ambos grupos fueran similares, se esperaría en cada uno un porcentaje de controlados similar al valor medio de los pacientes de los dos grupos juntos, esto es: 20% (8 controlados en total/40 pacientes en total). Entonces, si ello fuera así, en el grupo I tendría que haber 4 controlados (20*20%), y en el grupo (C) otros 4, con lo que se diseña otra tabla de contingencia, esta vez con los valores esperados. A continuación, con Excel se va a «Fórmulas – Funciones estadísticas – Prueba.Chi», lo cual ofrece un valor de p de 0,11285. Si aplicamos este valor en la función «Prueba.Chi.Inversa» (en la misma ubicación), el valor de chi estimado es de 2,5. Como el percentil 95 de la distribución de chi cuadrado con 1 grado de libertad es 3,84, y tenemos que 2,5 <3,84, podemos concluir que no hay diferencia significativa entre el grado de control de la hipertensión con y sin intervención, y que la diferencia observada puede deberse al azar (téngase en cuenta que en este ejemplo habría que haber practicado la corrección de Yates, al presentarse valores mínimos en algunas celdas de la tabla; no obstante, ello no habría modificado la conclusión final).
Conclusión
Tan importante como el diseño y la ejecución del estudio experimental es el correcto análisis de los resultados. Un incorrecto análisis lleva inexorablemente a unas conclusiones erróneas.
En la farmacia comunitaria se puede disponer sin dificultad de un programa como Microsoft Excel, con el que pueden resolverse muchos análisis básicos de estadística descriptiva e inferencial. Es decir, podemos estimar, de una manera bastante sencilla, los valores de los estimadores de las variables analizadas y someterlas a pruebas sencillas.
Dos pruebas básicas consisten en el análisis de las diferencias de medias y de proporciones. Los estudios que se lleven a la práctica poseerán variables de resultado que serán cuantitativas o cualitativas, mientras que la variable de exposición será cualitativa. Con este planteamiento básico pueden analizarse las primeras mediante la prueba de la t de Student, y las segundas con la de la chi al cuadrado.
Obviamente, en muchos casos se precisará de análisis estadísticos más sofisticados, para lo cual habría que recurrir a programas informáticos más complejos, como SPSS. En tales situaciones, la utilización de dichos programas requerirá la ayuda de profesionales especializados.
