En este artículo pretendemos ofrecer una vista panorámica de la topología molecular, que es una aplicación de la teoría de grafos muy utilizada en la industria química y, sobre todo, en la farmacéutica. El objetivo de la topología molecular es la caracterización estructural de moléculas mediante unos invariantes sencillos, llamados índices topológicos. Estos índices, una vez procesados estadísticamente, tienen un papel fundamental en el descubrimiento de nuevas aplicaciones de moléculas conocidas y en el diseño de moléculas con propiedades químicas y farmacológicas específicas.
Introducción a la topología molecular
La topología molecular está basada en la aplicación de la «teoría de grafos» a la descripción de estructuras moleculares. La teoría de grafos es al mismo tiempo una parte importante de la matemática aplicada, que fue introducida en 1874 por los matemáticos Silvester y Cayley1,2, y que se aplica básicamente a todos los campos de las ciencias experimentales, en particular al estudio de redes y sistemas complejos (red de comunicaciones, diseño de circuitos eléctricos, red de aprovisionamiento de materiales, y otras muchas aplicaciones actuales).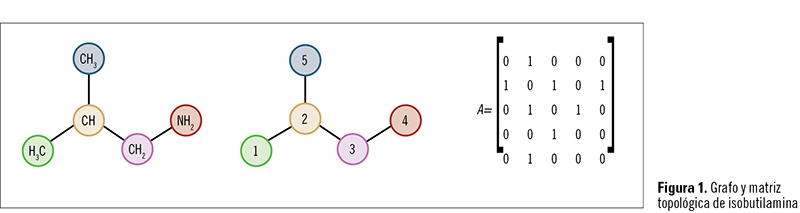 El grafo es un conjunto de objetos, llamados «puntos» o «vértices», conectados por enlaces, llamados «líneas» o «ejes». Cuando se aplica a las moléculas, los puntos desempeñan el papel de átomos y las líneas el de enlaces químicos (figura 1), normalmente covalentes, porque es en moléculas orgánicas donde este método encontró su principal aplicación.
El grafo es un conjunto de objetos, llamados «puntos» o «vértices», conectados por enlaces, llamados «líneas» o «ejes». Cuando se aplica a las moléculas, los puntos desempeñan el papel de átomos y las líneas el de enlaces químicos (figura 1), normalmente covalentes, porque es en moléculas orgánicas donde este método encontró su principal aplicación.
La clave del método radica en el conocimiento de qué átomo está enlazado con uno concreto y en el conocimiento del camino que debe seguirse de un átomo a otro en la misma molécula. El uso topológico de los índices o descriptores topológicos es caracterizar estructuralmente un compuesto. El primer paso para definir estos índices es representar los átomos por puntos llamados vértices y los enlaces por segmentos llamados ejes, eliminando los átomos de hidrógeno. Hay formulaciones alternativas que toman en consideración los átomos de hidrógeno, pero no serán analizadas en este artículo.
El grafo para una molécula se obtiene de esta manera. Los diferentes átomos, vértices, se numeran sucesivamente de una forma aleatoria, y la matriz topológica adyacente, cuyos elementos tij son uno o cero, se construye en función del hecho de que el átomo «i» pueda enlazarse o no con el átomo «j», respectivamente.
En la figura 1 se muestra la matriz topológica de isobutilamina.
A partir de esta matriz y de los algoritmos o procedimientos matemáticos adecuados, se obtienen los índices topológicos más importantes. Entre ellos, podemos destacar los autovalores de la matriz, los índices de Hosoya3, Randic4, Balaban5, Kier y Hall6, etc. Estos índices son, por tanto, descriptores numéricos de la estructura molecular, y constituyen una descripción matemática de las moléculas.
Una vez obtenidos los índices topológicos (IT) (para ello, pueden usarse algunos programas de ordenador comerciales), se procede a la obtención de ecuaciones que correlacionen las propiedades que se pretendan predecir y los IT. La idea es que dichas ecuaciones nos sirvan para predecir las propiedades de nuevos compuestos, es decir, de compuestos que no han sido utilizados para la obtención de las ecuaciones de correlación.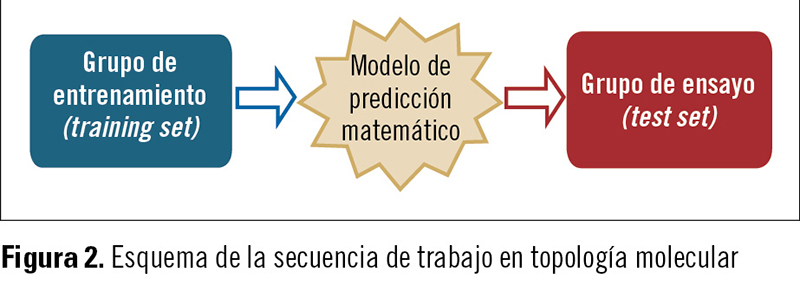 Los compuestos que se han utilizado en la obtención de las ecuaciones constituyen el llamado grupo de entrenamiento (training set), mientras que aquellos que no han sido incluidos forman el llamado grupo de ensayo (test set) (figura 2).
Los compuestos que se han utilizado en la obtención de las ecuaciones constituyen el llamado grupo de entrenamiento (training set), mientras que aquellos que no han sido incluidos forman el llamado grupo de ensayo (test set) (figura 2).
De este modo, las propiedades de compuestos conocidos nos sirven para predecir las de los desconocidos, que pueden incluso no haber sido sintetizados en el laboratorio y tener por tanto sólo una existencia virtual.
Las características singulares de la topología molecular pueden, por tanto, resumirse del siguiente modo:
a) Es una vía puramente matemática de describir la estructura molecular.
b) Es un método muy eficaz para descubrir nuevas moléculas activas barriendo bases de datos (screening, o cribado) y también para diseñar nuevas moléculas, dado que todo el proceso es fácilmente computarizable.
La segunda característica (b) es una consecuencia inmediata de la primera (a).
Análisis discriminante
Cuando se trata de seleccionar un nuevo fármaco, el primer problema que debemos afrontar es si realmente la nueva molécula va a presentar o no la actividad farmacológica esperada. Una vez que esto se haya garantizado, podremos –a través de las adecuadas ecuaciones– predecir características tales como absorción, biodisponibilidad, eliminación, toxicidad, etc.
Para afrontar el reto de garantizar que realmente el nuevo compuesto va a tener dicha actividad, se emplea el análisis lineal discriminante (ALD)7,8. El ALD es una técnica estadística cuyo fin es encontrar la función matemática que sea capaz de distinguir entre dos o más categorías u objetos. En nuestro caso, utilizaremos un grupo de entrenamiento constituido por compuestos activos e inactivos, calculando a continuación sus índices topológicos y encontrando la función matemática que distingue los activos de los inactivos.
Un aspecto capital en la obtención de una buena función discriminante es la selección del grupo de entrenamiento adecuado. Como antes señalábamos, el grupo está constituido por un subgrupo de compuestos activos y otro de compuestos inactivos. Sin embargo, ambos grupos deben diferir sólo en la actividad, y no en aspectos estructurales simples o constitutivos que hagan la discriminación trivial. Por ejemplo, si el grupo de los activos está formado por moléculas muy grandes y el de los inactivos por otras más pequeñas, el resultado vendrá dado por la diferencia de tamaños, y no de la actividad. Por tanto, ambos grupos han de estar formados por moléculas similares en tamaño, naturaleza química y otros elementos constitutivos (número y tipo de ciclos, grupos funcionales, etc.) que garanticen que la discriminación lo es sólo por la actividad.
Hay métodos reglados que garantizan este aspecto, particularmente los coeficientes que cuantifican el concepto de semejanza entre dos moléculas, entre los que destacaremos el de Tanimoto, el método del coseno y el de la distancia euclidiana, que se definen como:
Coeficiente de Tanimoto= Σ XiX j /(ΣXi2 + ΣXj2 – Σ XiXj)
Teorema del coseno= ΣXi Xj /(ΣXi2 ΣXj2 ) ½
Distancia euclidiana= (Σ(Xi – X j)2) ½
Donde Xi y Xj son los valores de los índices topológicos de las dos moléculas, i y j, que se quieren comparar. Valores próximos a 1 para el coeficiente de Tanimoto y 0 para la distancia euclidiana indicarían elevada semejanza topológica entre las moléculas i y j.
Redes neuronales artificiales
Estas redes se utilizan para el tratamiento de la información cuya unidad de procesado se inspira en la neurona biológica. La «red neuronal artificial» es un entramado de neuronas con una capacidad determinada de procesamiento que, debido a su alto grado de conexión, le proporciona al sistema neuronal una altísima capacidad de procesamiento paralelo, por lo que las «redes neuronales» son capaces de resolver problemas que de otro modo serían difíciles de estudiar.
La neurona artificial dispone de entradas y salidas de información. Las neuronas del cerebro humano tienen entradas preferentes de información según el tipo de estímulo al que responden, y esta preferencia se simula en las redes neuronales artificiales mediante los pesos. Esta ecuación encargada de tratar cada uno de estos pesos, multiplicados por el valor de la entrada de información, es la función de propagación, y define el estado interno de la neurona. En el presente estudio la función de propagación utilizada es una función de tipo sumador. El valor obtenido de la función de propagación se trata mediante la denominada «función de activación», que genera un valor de salida en la neurona. En este trabajo la función de activación utilizada es una función de tipo no lineal, la función tangencial.
Frank Rosenblatt comenzó en 1958 el desarrollo del perceptrón o máquina de aprendizaje, que es la red neuronal más antigua y capaz de entrenarse y reconocer una serie de patrones. Se diferencia de las computadoras en que el perceptrón es más flexible, ya que puede adaptarse a las situaciones no previstas por las instrucciones programadas9.
Para establecer una analogía entre la actividad neuronal humana y las redes artificiales, determinaremos que las señales que llegan a la sinapsis son las entradas, que son ponderadas, atenuadas o amplificadas por un parámetro que denominamos «peso». Estas entradas pueden excitar a la neurona por su peso positivo, o inhibirla por su peso negativo. La suma de las entradas ponderadas es el efecto; la neurona se activa si la suma es mayor que el umbral. Y las señales se ajustan por un mecanismo de aprendizaje.
La regla de propagación combina los valores de entrada a una neurona con los pesos de las conexiones que llegan a ésta. Y también se necesita una regla que combine las entradas con el estado actual de la neurona para producir un nuevo estado de activación. Esta función de activación puede ser de tipo escalón, lineal o de identidad, lineal mixta o sigmoidal.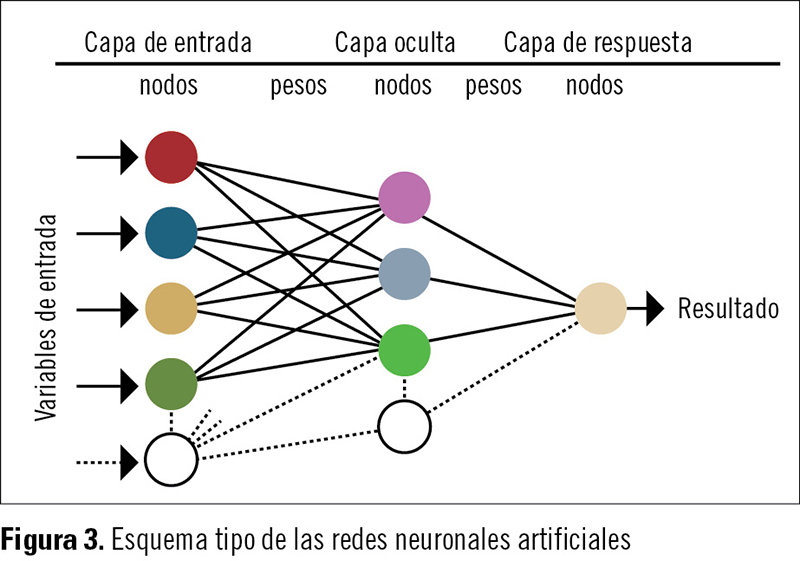 La estructura de su organización consta de tres capas de elementos básicos –recibe el nombre de «unidad umbral lógica» (TLU, por sus siglas en inglés, Threshold Logic Unit)–, que son unidades binarias que suman los pesos de las señales de entrada y se excitan sólo si la suma de estos pesos sobrepasa los valores umbrales prescritos. La primera capa de entrada o sensora (o «S») está compuesta por unidades sensoriales que, en nuestro caso, son los cientos de índices topológicos utilizados que están conectados con una segunda capa de TLU compuesta de «unidades de asociación» (o «A»), que es una capa llamada oculta porque, a diferencia de la tercera y última «capa de respuesta» (o «R») (figura 3), recibe señales de entrada fijas; la capa de respuesta recibe intensidades o valores regulables y cambiantes conforme se va produciendo el entrenamiento de las redes. Las únicas salidas que vamos a dar son +1 y –1, es decir, análogo al disulfiram o no análogo al disulfiram en nuestro estudio. Para ello, necesitamos un método de adiestramiento que nos permitirá adaptar los pesos de las entradas de A a las unidades R, y obtener así la respuesta correcta en cada situación, después de haber aprendido a discriminar.
La estructura de su organización consta de tres capas de elementos básicos –recibe el nombre de «unidad umbral lógica» (TLU, por sus siglas en inglés, Threshold Logic Unit)–, que son unidades binarias que suman los pesos de las señales de entrada y se excitan sólo si la suma de estos pesos sobrepasa los valores umbrales prescritos. La primera capa de entrada o sensora (o «S») está compuesta por unidades sensoriales que, en nuestro caso, son los cientos de índices topológicos utilizados que están conectados con una segunda capa de TLU compuesta de «unidades de asociación» (o «A»), que es una capa llamada oculta porque, a diferencia de la tercera y última «capa de respuesta» (o «R») (figura 3), recibe señales de entrada fijas; la capa de respuesta recibe intensidades o valores regulables y cambiantes conforme se va produciendo el entrenamiento de las redes. Las únicas salidas que vamos a dar son +1 y –1, es decir, análogo al disulfiram o no análogo al disulfiram en nuestro estudio. Para ello, necesitamos un método de adiestramiento que nos permitirá adaptar los pesos de las entradas de A a las unidades R, y obtener así la respuesta correcta en cada situación, después de haber aprendido a discriminar.
Los métodos QSAR se han desarrollado tradicionalmente utilizando métodos de regresión lineal. La gran ventaja de las redes neuronales es que son capaces de reconocer relaciones no lineales.
Procedimiento en R versión 3.0.1
R versión 3.0.1 es un proyecto colaborativo y gratuito que pertenece a The R Foundation for Statistical Computing. R 3.0.1 es un software que requiere unas mínimas habilidades de programación y, a través de distintos comandos, permite conocer al usuario exactamente cada paso del análisis.
Por otro lado, precisa del cumplimiento de unas restricciones matemáticas para poder realizar el análisis discriminante. Asimismo, requiere de una preparación de los datos exhaustiva. Esto supone, entre otras premisas, rechazar las variables colineales, ya que no aportan información al modelo que se pretende crear.
Una vez importados los datos, lo primero es analizar la igualdad de las medias de los grupos a través de un test de Wilks. Si el valor de Pr es inferior a 0,05, habrá diferencias entre las medias y el análisis discriminante es aplicable. De esta forma, la variable que mayor poder discriminante tiene es la que presenta menor Pr (probabilidad en el test de Wilks) o mayor valor de F.
R 3.0.1 nos facilita unos primeros resultados de clasificación del grupo de entrenamiento y una validación cruzada de este grupo a posteriori.
Una vez obtenido el modelo con los coeficientes de las funciones canónicas discriminantes, que en este caso son tantos como variables se han incluido en el análisis, se procede a validarlo con el grupo test de moléculas. El modelo nos servirá para identificar moléculas análogas en la búsqueda guiada.
Ejemplo de búsqueda de nuevas terapias
Análogos de disulfiram
El disulfiram se utiliza para el tratamiento del alcoholismo crónico, y produce una reacción adversa al consumir etanol. Las siguientes son algunas de las moléculas análogas de disulfiram, como el tetraetiltiuram disulfuro, y que están ya en uso o en avanzada fase de investigación: coprina (N5-1-hidroxiciclopropil-L-glutamina), que se metaboliza a 1-aminociclopropanol; temposil o carbamida cálcica cítrica, que tiene los mismos efectos que el disulfiram, pero es más suave y seguro; clorpropamida, que es una sulfonilurea; tetrametiltiuram monosulfuro; metil NN-dietilditiocarbamato, y metileno bis-(NN-dietilditiocarbamato).
Resultados de la selección de nuevos análogos de disulfiram
Ilustramos a continuación los resultados obtenidos en las ecuaciones de correlación y en la selección de moléculas activas.
Obtención de los índices topológicos y de las ecuaciones de correlación
Para el cálculo de los índices topológicos, se emplearon dos programas comerciales: el PaDEL-Descriptor10 y el Dragon11. Los índices topológicos que intervienen en cada ecuación han sido etiquetados como IT1, IT2, IT3, IT4 e IT5.
Las ecuaciones de correlación se obtuvieron a través del programa SPSS12.
Las funciones discriminantes obtenidas fueron:
• FD (Dragon)= 0,014 IT1 - 17,8 IT2 - 2,33
Lambda de Wilks= 0,506; F= 26,85; grado medio de acierto= 81%.
• FD (PaDEL-Descriptor)= 0,189 IT3 - 0,67 IT4 + 3,28
Lambda de Wilks= 0,643; F= 14,98; grado medio de acierto= 73,7%.
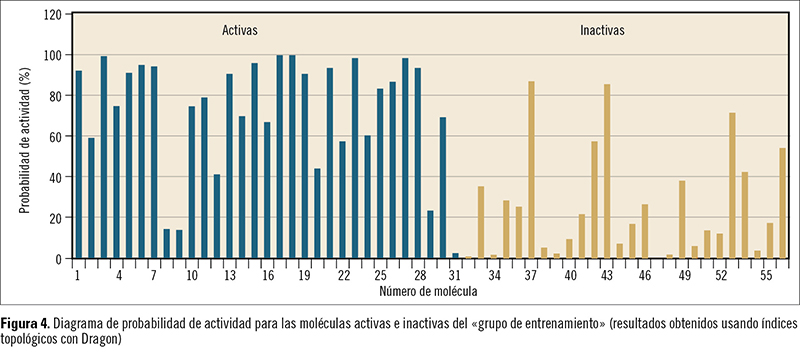 La figura 4 muestra el diagrama de probabilidad de actividad para las moléculas activas e inactivas del grupo de entrenamiento obtenido con el programa Dragon. Obsérvese que la gran mayoría de las activas muestran probabilidades superiores al 50%, mientras que la mayoría de las inactivas muestran valores inferiores al 50% (frecuentemente inferiores incluso al 25%).
La figura 4 muestra el diagrama de probabilidad de actividad para las moléculas activas e inactivas del grupo de entrenamiento obtenido con el programa Dragon. Obsérvese que la gran mayoría de las activas muestran probabilidades superiores al 50%, mientras que la mayoría de las inactivas muestran valores inferiores al 50% (frecuentemente inferiores incluso al 25%).
El objetivo último de la topología molecular es el establecimiento de ecuaciones de correlación entre propiedades moleculares e índices topológicos. Para ello, suele utilizarse el análisis lineal discriminante, introducido por Fisher en 1936, si bien algunos autores prefieren técnicas no lineales, como redes neuronales. Nosotros nos limitaremos al análisis lineal por ser el más extendido y, por tanto, el mejor contrastado.
El objetivo del análisis discriminante es encontrar una función capaz de distinguir (o discriminar, de ahí el nombre) entre dos o más categorías o grupos de objetos. La capacidad discriminante se mide determinando el porcentaje de objetos clasificados correctamente dentro de cada grupo. En la práctica, el análisis discriminante se realiza mediante alguno de los paquetes estadísticos disponibles en el mercado (SPSS, STATISTICA, etc.). La selección de los descriptores se basa en el parámetro F-Snedecor, y el criterio de clasificación es la menor distancia de Mahalanobis, que es la distancia entre el valor individual y el valor medio global que aparece en la ecuación de regresión. El programa estadístico elige las variables usadas en la computación de las funciones de clasificación (normalmente lineal) paso a paso: en cada una de estas fases, la variable que aporta más a la separación de los grupos se introduce en la función de discriminación, mientras que la que aporta menos se elimina. La calidad de la función de discriminación se evalúa con el parámetro lambda de Wilks (llamado también U-estadístico), empleando el test de igualdad de las medias de grupo para las variables de la función de discriminación.
 Moléculas seleccionadas
Moléculas seleccionadas
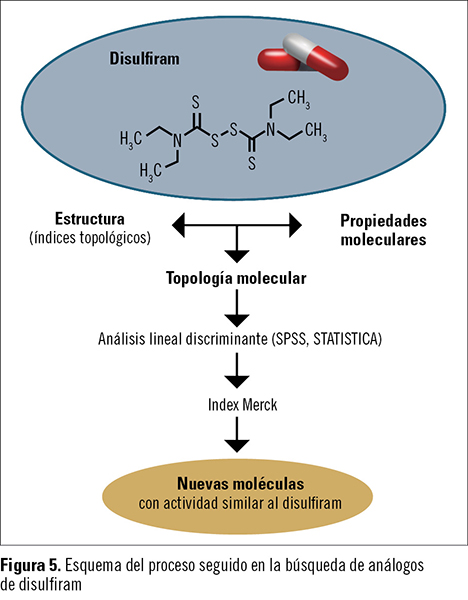
Con estas funciones, se rastreó el Index Merck (alrededor de 12.000 compuestos) y se seleccionaron varias moléculas con actividad similar al disulfiram (figura 5).
Aunque no se pretende aquí una búsqueda que garantice la actividad de las moléculas –lo que requiere un estudio mucho más exhaustivo–, la diversidad estructural de las moléculas seleccionadas resulta interesante, ya que es una fuente para posteriores refinamientos que nos permitan obtener nuevos «cabezas de serie». Alguna molécula puede constituir un nuevo lead y fuente de nuevas estructuras obtenidas por farmacomodulación.
Éstas son algunas de las moléculas seleccionadas con actividad similar al disulfiram: mercaptobenzotiazol, glibenclamida, gliclazida y tolbutamida.
Estas y otras muchas aplicaciones de la topología molecular se mencionan en muchos de nuestros trabajos13,14.
Conclusión
En este artículo hemos pretendido ilustrar el procedimiento de obtención, basado en la topología molecular, de nuevas moléculas potencialmente similares al disulfiram o Antabus©, llegándose a buenas ecuaciones de regresión que pueden permitir la selección de varios compuestos del Index Merck, de los que no había descrita la actividad buscada, y para los que los modelos topológicos utilizados predicen una significativa actividad similar al disulfiram.
Bibliografía
1. Silvester JJ. On the application of the new atomic theory to graphical representations of covariants of binary quantities. Am J Math. 1874; 1: 64-125.
2. Cayley A. On the mathematical theory of isomers. Phil Mag. 1874; 67: 444-446.
3. Hosoya H. Topological index. A newly proposed quantity characterizing the topological nature of structural isomers of saturated hydrocarbons. Bull Chem Soc Japan. 1971; 44(9): 2.332-2.339.
4. Randic M. Characterization of molecular branching. I. J Am Chem Soc. 1975; 97: 6.609-6.615.
5. Balaban AT. Distance Connectivity Index. Chem Phys Lett. 1982; 89(5): 399-404.
6. Kier LB, Hall LH. Molecular Connectivity in Chemistry and Drug Research. Nueva York: Academic Press, 1976.
7. Deakin EB. A discriminant analysis of predictors of business failure. J Account Research. 1976; 10(1): 167-180.
8. Gálvez J, García-Doménech R, Gregorio Alapont C, Julián-Ortiz JV, Popa L. Pharmacological distribution diagrams: a tool for de novo drug design. J Mol Graph. 1996; 14(5): 272-276.
9. Rosenblatt F. The Perceptron: a probabilistic model for information storage and organization in the brain. Psychol Review. 1958; 65: 386-408.
10. Yap CW. PaDEL-Descriptor: an open source software to calculate molecular descriptors and fingerprints. J Comput Chem. 2011; 32 (7): 1.466-1.474.
11. Dragon software. TALETE srl. Via V. Pisani, 13. 20124 Milano, Italy.
12. IBM Corp. Released (2010). IBM SPSS Statistics for Windows, versión 19.0. Armonk, NY: IBM Corp.
13. Amigó JM, Falcó A, Gálvez J, Villar V. Topología Molecular. Bol Soc Esp Mat Apl. 2007; 39: 137-151.
14. García-Doménech R, Gálvez J, de Julián-Ortiz JV, Pogliani L. Some new trends in chemical graph theory. Chemical Reviews. 2008; 108(3): 1.127-1.169.

